Ας γνωρίσουμε το Πείραμα του Ερατοσθένη

Το φως ως πειραματικό εργαλείο 2200 χρόνια π.Χ. Ένα από τα ωραιότερα πειράματα όλων των εποχών: το πείραμα του Ερατοσθένη

Ο Ερατοσθένης (Κυρήνη 276π.Χ. -Αλεξάνδρεια 194π.Χ.) ήταν αρχαίος Έλληνας μαθηματικός, γεωγράφος και αστρονόμος.

Θεωρείται ο πρώτος που υπολόγισε το μέγεθος της Γης και κατασκεύασε ένα σύστημα συντεταγμένων με παράλληλους και μεσημβρινούς. Αν και γεννήθηκε στην Κυρήνη (στη σημερινή Λιβύη), έζησε και εργάστηκε και πέθανε στην  πρωτεύουσα της πτολεμαϊκής Αιγύπτου, την Αλεξάνδρεια, όπου και σπούδασε, αν και πραγματοποίησε σπουδές και στην Αθήνα. Το 236 π.Χ. ορίστηκε από τον Πτολεμαίο τον Γ΄ τον Ευεργέτη βιβλιοθηκάριος της βιβλιοθήκης της Αλεξάνδρειας, διαδεχόμενος τον Ζηνόδοτο.

Η φαντασία οδηγός σε μια απλή παρατήρηση

  Μελετώντας έναν πάπυρο στη βιβλιοθήκη της Αλεξάνδρειας, διάβασε μια καταχώρηση η οποία του κέντρισε το ενδιαφέρον. Διάβασε, ότι στις 22 Ιουνίου την ημέρα δηλαδή του θερινού ηλιοστάσιου, στην πόλη Συήνη (το σημερινό Ασουάν) της Αιγύπτου, 800 περίπου χιλιόμετρα από την Αλεξάνδρεια συμβαίνει κάτι αξιοσημείωτο. Καθώς πλησιάζει το μεσημέρι οι σκιές των κιόνων ή μιας ράβδου μικραίνουν.

Στις 12 το μεσημέρι όταν δηλαδή ο ήλιος βρίσκεται στο ζενίθ, οι σκιές εξαφανίζονταν τελείως και το νερό καθρεπτίζεται στο πάτο ενός πηγαδιού. Ο Ήλιος δηλαδή, βρισκόταν ακριβώς κάθετα πάνω από τη περιοχή. Τι το ιδιαίτερο είχε όμως αυτή η απλή παρατήρηση ώστε να τραβήξει το ενδιαφέρον του Ερατοσθένη;

Οι περισσότεροι άνθρωποι θα αδιαφορούσαν για μια τέτοιου είδους ασήμαντη, καθημερινή πληροφορία. Ο Ερατοσθένης όμως δεν ήταν ένας τυχαίος άνθρωπος. Ως γνήσιος ερευνητής αναρωτήθηκε, πως είναι δυνατόν την ίδια ακριβώς στιγμή μια ράβδος να μην έχει σκιά στη πόλη της Συήνης, ενώ 800 περίπου χιλιόμετρα πιο κάτω, στην Αλεξάνδρεια, μια ράβδος ίδιου ύψους να έχει σκιά;  

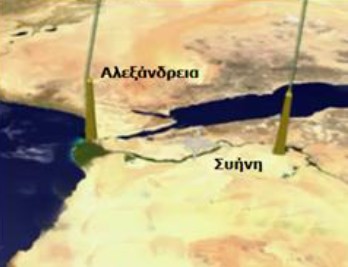
 Ο Ερατοσθένης σκέφτηκε ότι αν η Γη ήταν επίπεδη, τότε ο Ήλιος θα έριχνε τις ακτίνες του κάθετα και στις δυο πόλεις ταυτόχρονα υπό την ίδια γωνία. Συνεπώς καμία από τις δυο ράβδους δεν θα έπρεπε να έχει σκιά. Γενικότερα, αν η Γη ήταν επίπεδη, η σκιά στη Συήνη θα έπρεπε να έχει πάντα το ίδιο μήκος με αυτή στην Αλεξάνδρεια. Ο Ερατοσθένης λοιπόν συμπέρανε ότι για να μην έχει καθόλου σκιά η ράβδος στη Συήνη, ενώ την ίδια στιγμή στην Αλεξάνδρεια μια άλλη ίδια ράβδος έχει σκιά, δεν μπορεί παρά να σημαίνει ότι η επιφάνεια της Γης δεν είναι επίπεδη αλλά καμπύλη. Μάλιστα όσο πιο μεγάλη η καμπύλη τόσο πιο μεγάλη η διαφορά ανάμεσα στα μήκη των σκιών.

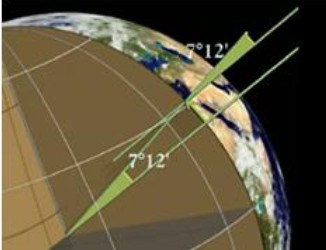Με αυτή λοιπόν την απλή παρατήρηση ο Ερατοσθένης έφτασε στο συμπέρασμα ότι η Γη είναι σφαιρική και όχι επίπεδη. Μέτρησε μάλιστα το μήκος της σκιάς της ράβδου και από τη μέτρηση αυτή είδε ότι οι ακτίνες του ήλιου σχημάτιζαν με τη κάθετη ράβδο μια γωνία 7ο12'  δηλαδή το 1/50 ενός πλήρους κύκλου. Aν προεκτείνουμε μάλιστα τις ράβδους στη Συήνη και την Αλεξάνδρεια  προς το κέντρο της Γης βλέπουμε ότι η γωνιακή απόσταση μεταξύ των δυο πόλεων είναι 7ο 12'.

Ο Ερατοσθένης προσέλαβε βηματιστές που μέτρησαν την απόσταση μεταξύ της Αλεξάνδρειας και της Συήνης και τη βρήκαν 5000 στάδια. Αν η γωνία λοιπόν των 7ο 12' αντιστοιχούσε σε απόσταση 5000 στάδια, ο Ερατοσθένης με απλά μαθηματικά υπολόγισε ότι η περιφέρεια της Γης πρέπει να είναι 252.000 στάδια δηλαδή 39.690 χιλιόμετρα.

Ο Ερατοσθένης με μόνα εργαλεία τη σκέψη του και μια ράβδο κατάφερε να μετρήσει 2.200 χρόνια πριν τη περίμετρο της Γης με εντυπωσιακή ακρίβεια. Δεδομένου ότι η πραγματική τιμή της περιφέρειας της Γης στον Ισημερινό είναι 40.075 χιλιόμετρα η απόκλιση των μόλις 385 χιλιομέτρων της μέτρησης του Ερατοσθένη από τη πραγματική τιμή είναι αξιοσημείωτη.

Το πείραμα μπορεί να επαναληφθεί

   Το πείραμα του Ερατοσθένη μπορεί να διεξαχθεί ανάμεσα σε δυο οποιεσδήποτε περιοχές. Σε κάθε περίπτωση αυτό που χρειάζεται να γνωρίζουμε είναι η γωνιακή απόσταση μεταξύ των δυο περιοχών καθώς και η απόστασή τους μετρημένη στον ίδιο μεσημβρινό. Δεδομένου ότι καμία από τις δυο περιοχές που θα χρησιμοποιήσουμε για τη δική μας μέτρηση δεν είναι η Συήνη, η μέτρηση της σκιάς της ράβδου θα πρέπει να γίνει και στις δυο περιοχές.

   Και για τις δυο περιοχές θα βρούμε τη γωνία όπως έκανε και ο Ερατοσθένης και στη συνέχεια θα αφαιρέσουμε τις δυο γωνίες για να βρούμε τη γωνιακή απόσταση μεταξύ των περιοχών. Οι δυο μετρήσεις για τον υπολογισμό της γωνιακής απόστασης πρέπει να γίνουν την ίδια μέρα και κάτω από τις ίδιες συνθήκες δηλαδή όταν ο ήλιος βρίσκεται στο ζενίθ για κάθε περιοχή. 

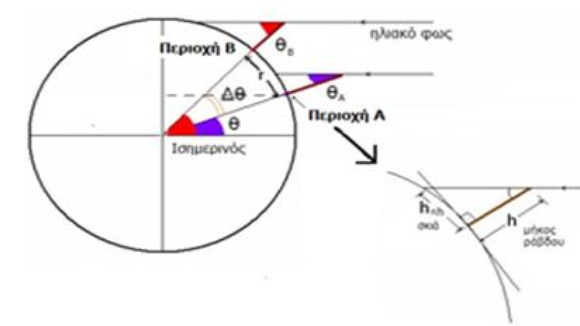
Ο υπολογισμός αυτός γίνετε όπως τον έκανε και ο Ερατοσθένης πριν περίπου 2200 χρόνια. Τοποθετούμε μια ράβδο κάθετα στο έδαφος. Βρίσκουμε την ώρα που ο ήλιος βρίσκεται στο ζενίθ και εκείνη τη χρονική στιγμή μετράμε τη σκιά της. Όταν ο Ήλιος βρίσκεται στο ζενίθ η σκιά της ράβδου είναι η μικρότερη δυνατή. Μετράμε επίσης και το μήκος της ράβδου. Η ράβδος, η σκιά της και οι ακτίνες του Ήλιου σχηματίζουν ένα ορθογώνιο τρίγωνο. Η γωνία θ μεταξύ των ηλιακών ακτινών και της ράβδου είναι η γωνιακή απόσταση του τόπου από τον Ισημερινό.

Η γωνία Δθ είναι η γωνιάκη απόσταση μεταξύ των δυο περιοχών.

Ο Ερατοσθένης στο σχολείο μας

Το σχολείο μας συμμετέχει και φέτος στα eTwinning έργα Eratosthenes (2020 και 2021) με ιδρυτή τον Γάλλο εκπαιδευτικό ο κ. Eric Vayssie. Στις 20 Μαρτίου 2021 κάναμε την πιο κοντινή στην εαρινή ισημερία μέτρησή μας, όπως και τα άλλα 23 σχολεία από τις 4 ηπείρους της υδρογείου, που συμμετέχουν στο Εratosthenes 2021. Ο ακριβέστερος υπολογισμός για το σχολείο μας, έγινε ταιριάζοντας τα δεδομένα μας με αυτά Alta Gracia, Argentina. Τα αποτελέσματα για την εαρινή Ισημερία μπορείτε να δείτε εδώ

 Οι μετρήσεις και η συνεργασία του σχολείου μας με τα υπόλοιπα σχολεία θα συνεχιστούν για όλο το υπόλοιπο 2021. Άμεσα σχέδια: μέτρηση για το Θερινό Ηλιοστάσιο στις 21 Ιουνίου, οπότε τα δεδομένα μας θα σταλούν στην Βιβλιοθήκη της Αλεξάνδρειας για να χρησιμοποιηθούν στην εκδήλωση-αφιέρωμα στο ιστορικό πείραμα που θα πραγματοποιηθεί και φέτος 

Και βέβαια θα σας κρατάμε ενήμερους για ότι νέο.

• < Προηγούμενο